从垂直到垂直

denglongshan

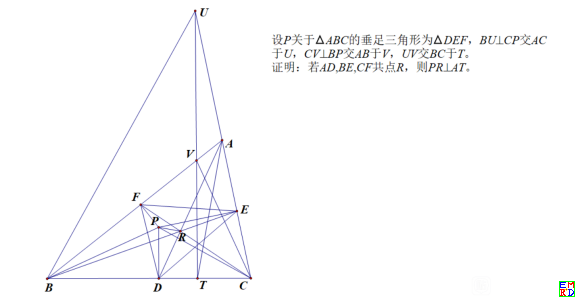
百度贴吧难题
贴吧网友qzc的解答：
只要证明这个结论：
S_1S_2S_3是S关于△ABC的塞瓦三角形,BU,CV分别平行S_1S_2,S_1S_3交对边于U,V.UV交BC于T,则AT平行S的三线性极线.
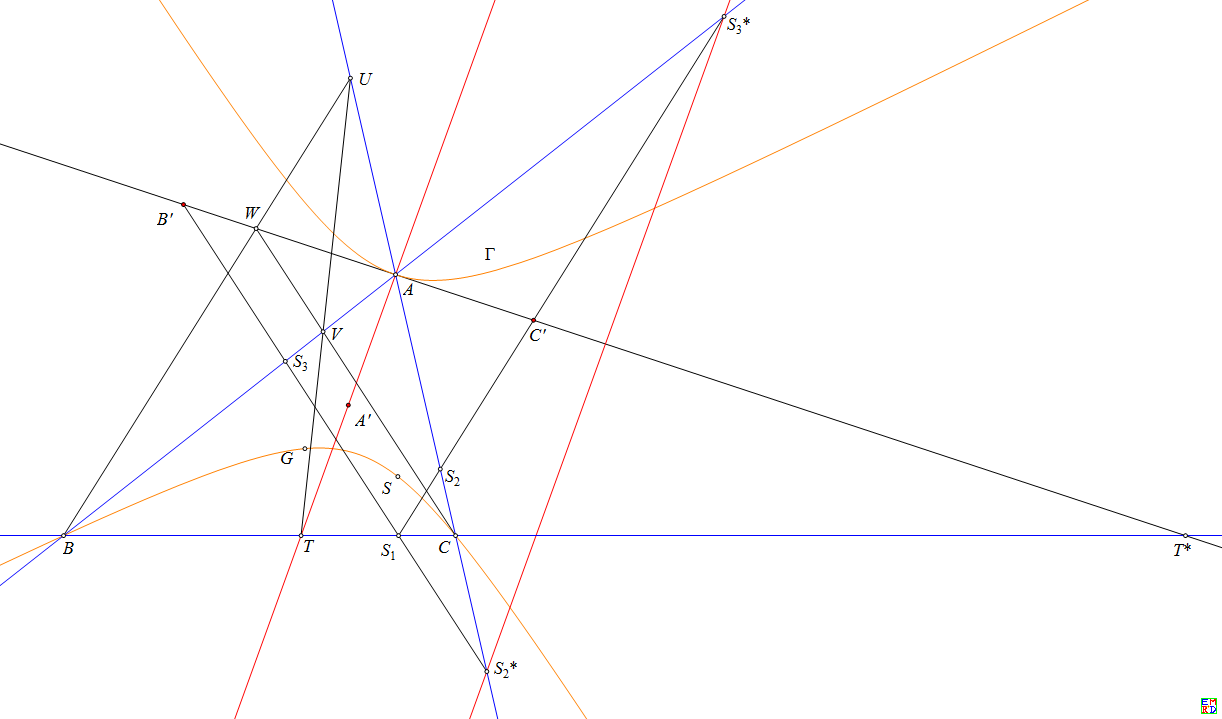
证明：设BU∩CV=W，G为△ABC的重心，作过A,B,C,G,S的二次曲线Γ，设A,B,C关于Γ的极点分别为A',B',C'，则A'在S_2S_3上等.下面证明W∈B'C'.
让S在Γ上运动,则BU∩B'C'→C'S_2→BS→S→CV∩B'C'是射影对应,则只要考虑三种情况使它们相等.
当S=G时显然成立.
当S=C时,BU∥CC',故BU=BB',CV∥CB',故CU=CB',此时结论成立
当S=B时同上可知结论成立
设B'C'∩BC=T*,则由W∈B'C'知[B,C;T,T*]=-1,故A,A',T共线,故AT和S的三线性极线平行.

证明太难，没有看懂

denglongshan

证明：设BU∩CV=W，G为△ABC的重心，作过A,B,C,G,S的二次曲线Γ，设A,B,C关于Γ的极点分别为A',B',C'，则A'在S_2S_3上等.下面证明W∈B'C'.，很难理解