举例说明：随机变量 X,Y 不相关，满足 E(XY)=E(X)E(Y)，但 X,Y 有可能不相互独立

wufaxian

E(XY)=E(X)E(Y)无法推出随机变量X与Y互相独立？

事情的起因：

独立=>相关系数为0

逆否命题：相关系数不为0=>不独立（或者相关）

相关系数为0=>可以是独立也可以是不独立，我们不能得出任何有价值的结论


1、独立=>相关系数为0    因为X与Y互相独立=>存在E(XY)=E(X)E(Y) （注：在证明E(XY)=E(X)E(Y)过程中用到P(XY)=P(X)P(Y),所以若XY不独立则无法推出 E(XY)=E(X)E(Y)）
    E(XY)=E(X)E(Y)=>Cov(X,Y)=0 证明过程如下：
     

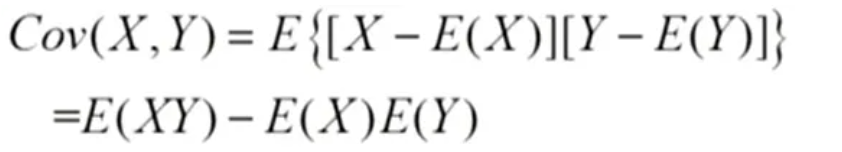
     由上可知:独立=>相关系数为0 成立

2、相关系数为0=>可以是独立也可以是不独立，我们不能得出任何有价值的结论
     相关系数为0=>Cov(X,Y)=0=>E(XY)=E(X)E(Y)  如果“相关系数为0=>可以是独立也可以是不独立，我们不能得出任何有价值的结论”等价于E(XY)=E(X)E(Y)  无法=> X,Y 互相独立？ 进一步当X，Y不是互相独立的时候也有可能存在E(XY)=E(X)E(Y)？
请问红字部分的结论容易证明么？我找不到相关的证明。还请老师指教。



备注：事情的起因是证明《精通计量》p26“和的方差等于方差的和” 成立的前提条件“XY 独立或不相关”
[

luyuanhong