ABC,BDC 是全等正三角形，O 是 ΔABC 中心，F 是 AE 中点，证明：OF⊥DF，∠OFD=60°

denglongshan

uk702 发表于 2021-11-3 08:22
\( 设\ C\ 为原点，\ 则 \ A=Be^{\frac{-i\pi}{3}}, \  E=De^{\frac{i\pi}{3}} \)
\( 求得\ G=\frac{A+B+C ...

\(设B在原点，d=1,\omega = 0; d = 1; e = 1 + \omega， b = a (1 + \omega); f = (b + d)/2， g = (a + b)/3\)，手工计算也不难

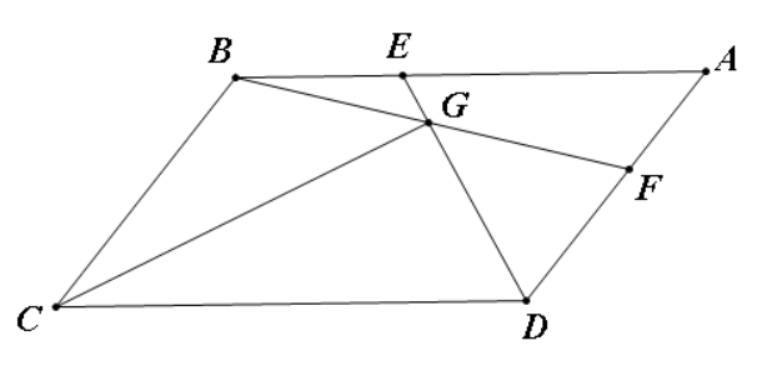
设\(d=1,v=e^{iBCD},b=rv,\overrightarrow{DF}=r1v{,}\overrightarrow{BE}=r1\)，求复数直线方程可得G，手工算可能有些费力，复数比坐标这类问题会更简便，不知道你想得到的简便效果是什么？可以试试内角平分线定理。

楼主注意下面的链接，可以发掘更多结论。
楼主老师的原帖

uk702

denglongshan 发表于 2021-11-4 21:25
\(设B在原点，d=1,\omega = 0; d = 1; e = 1 + \omega， b = a (1 + \omega); f = (b + d)/2， g = (a  ...

老师才是真正的行家！至于该题最简单的证明，我见过最简单的证明是一行字（解答应该是来自 Kuning 的初等数学论坛吧）。

不纠结了，相信你的方法是大方向，最终还是计算打败各种各样的技巧，机器的自动证明更是一座山峰。

uk702

denglongshan 发表于 2021-11-4 21:25
\(设B在原点，d=1,\omega = 0; d = 1; e = 1 + \omega， b = a (1 + \omega); f = (b + d)/2， g = (a  ...

知乎上的这篇文章很不错，适合我这种水平的人学习：
复数与几何（二） 直线与圆
https:\//zhuanlan.zhihu.com/p/158803422

denglongshan

uk702 发表于 2021-11-4 22:50
老师才是真正的行家！至于该题最简单的证明，我见过最简单的证明是一行字（解答应该是来自 Kuning 的初 ...

过奖！虽然没有技术含量，不知道公理方法是否容易？

uk702

denglongshan 发表于 2021-11-6 20:19
过奖！虽然没有技术含量，不知道公理方法是否容易？

非常感谢！收获甚丰，这次总算把套路搞明白了。