H,O是ΔABC的垂心和外心，D,E,F是垂足。AD交⊙O于P，陪位中线交⊙O于Q，证明EFPQ共圆

天山草

denglongshan

1. 
   
2. \!\(\*OverscriptBox["a", "_"]\) = 1/a;
   
3. \!\(\*OverscriptBox["b", "_"]\) = 1/b;
   
4. \!\(\*OverscriptBox["c", "_"]\) = 1/c; m = (b + c)/2;
   
5. \!\(\*OverscriptBox["m", "_"]\) = (
   
6. \!\(\*OverscriptBox["b", "_"]\) +
   
7. \!\(\*OverscriptBox["c", "_"]\))/2;
   
8. KAB[a_, b_] := (a - b)/(
   
9. \!\(\*OverscriptBox["a", "_"]\) -
   
10. \!\(\*OverscriptBox["b", "_"]\));
    
11. \!\(\*OverscriptBox["KAB", "_"]\)[a_, b_] := 1/KAB[a, b];(*复斜率定义*)
    
12. KAB[a_, b_, c_] := KAB[a, b]/KAB[b, c];(*e^(2iB) 等于复斜率相除*)
    
13. 
    
14. \!\(\*OverscriptBox["Jd", "_"]\)[k1_, a1_, k2_, a2_] := -((a1 - k1
    
15. \!\(\*OverscriptBox["a1", "_"]\) - (a2 - k2
    
16. \!\(\*OverscriptBox["a2", "_"]\)))/(
    
17.   k1 - k2));(*复斜率等于k1,过点A1与复斜率等于k2,过点A2的直线交点*)
    
18. Jd[k1_, a1_, k2_, a2_] := -((k2 (a1 - k1
    
19. \!\(\*OverscriptBox["a1", "_"]\)) - k1 (a2 - k2
    
20. \!\(\*OverscriptBox["a2", "_"]\)))/(k1 - k2));
    
21. e = Jd[-a c, a, a c , b];
    
22. \!\(\*OverscriptBox["e", "_"]\) =
    
23. \!\(\*OverscriptBox["Jd", "_"]\)[-a c, a, a c , b];
    
24. f = Jd[-a b, a, a b , c];
    
25. \!\(\*OverscriptBox["f", "_"]\) =
    
26. \!\(\*OverscriptBox["Jd", "_"]\)[-a b, a, a b , c];
    
27. p = (-b c)/a;
    
28. \!\(\*OverscriptBox["p", "_"]\) = 1/p;
    
29. q = -((a b c)/KAB[m, a]);
    
30. \!\(\*OverscriptBox["q", "_"]\) = 1/q;
    
31. Simplify[{1, p, ,
    
32. \!\(\*OverscriptBox["p", "_"]\), q,
    
33. \!\(\*OverscriptBox["q", "_"]\)}]
    
34. Simplify[{2, KAB[f, q], KAB[f, p], , KAB[e, q], KAB[e, p]}]
    
35. Simplify[{3, KAB[q, f, p], KAB[q, e, p]}](*角度验证*)
    
36. Simplify[KAB[q, f, p] == KAB[q, e, p]]
    
37. Simplify[{q - f, p - f, , (q - f)/(p - f), , q - e, p - e, , (q - e)/(
    
38.   p - e)}]
    
39. Simplify[{(q - f)/(p - f)/(q - e)/(p - e), (
    
40. \!\(\*OverscriptBox["q", "_"]\) -
    
41. \!\(\*OverscriptBox["f", "_"]\))/(
    
42. \!\(\*OverscriptBox["p", "_"]\) -
    
43. \!\(\*OverscriptBox["f", "_"]\))/(
    
44. \!\(\*OverscriptBox["q", "_"]\) -
    
45. \!\(\*OverscriptBox["e", "_"]\))/(
    
46. \!\(\*OverscriptBox["p", "_"]\) -
    
47. \!\(\*OverscriptBox["e", "_"]\))}]
    
48. Simplify[(q - f)/(p - f)/(q - e)/(p - e) == (
    
49. \!\(\*OverscriptBox["q", "_"]\) -
    
50. \!\(\*OverscriptBox["f", "_"]\))/(
    
51. \!\(\*OverscriptBox["p", "_"]\) -
    
52. \!\(\*OverscriptBox["f", "_"]\))/(
    
53. \!\(\*OverscriptBox["q", "_"]\) -
    
54. \!\(\*OverscriptBox["e", "_"]\))/(
    
55. \!\(\*OverscriptBox["p", "_"]\) -
    
56. \!\(\*OverscriptBox["e", "_"]\))]
    

复制代码

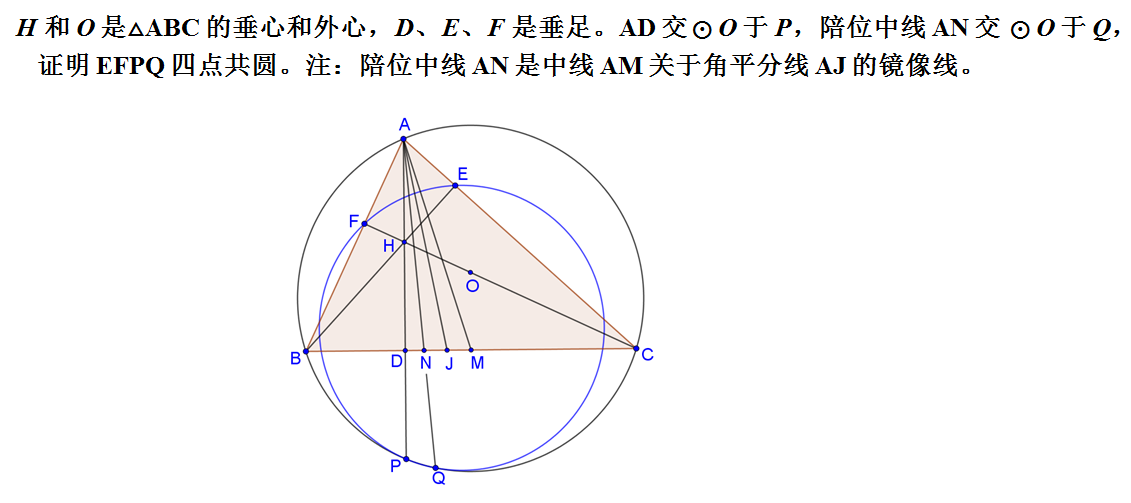
无论用角度或交比验证，可以进一步发现计算结果表示的几何意义，即发现新的结论。

天山草

程序代码：

1. Clear["Global`*"]; (*令\[CapitalDelta]ABC的外接圆为单位圆O，BC边平行于实轴，再令 AB、AC的复斜率分别为 u^2、v^2*)
   
2. \!\(\*OverscriptBox[\(o\), \(_\)]\) = o = 0;  a = I u v;   \!\(\*OverscriptBox[\(a\), \(_\)]\) = 1/(I u v); b = (I u)/v;  
   
3. \!\(\*OverscriptBox[\(b\), \(_\)]\) = v/(I u);  c = (I v)/u;  \!\(\*OverscriptBox[\(c\), \(_\)]\) = u/(I v);
   
4. h = (I ((v^2 + 1) u^2 + v^2))/(u v); \!\(\*OverscriptBox[\(h\), \(_\)]\) = -((I (u^2 + v^2 + 1))/(  u v)); j = (I (u^2 + u v + v^2 - 1))/(u v + 1); \!\(\*OverscriptBox[\(j\), \(_\)]\) = ( I (u^2 (v^2 - 1) - u v - v^2))/(u v (u v + 1));
   
5. Jx[p_, a_, b_] := (\!\(\*OverscriptBox[\(a\), \(_\)]\) b - a \!\(\*OverscriptBox[\(b\), \(_\)]\) + \!\(\*OverscriptBox[\(p\), \(_\)]\) (a - b))/(\!\(\*OverscriptBox[\(a\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\));(*P点的镜线，镜线过已知点 A、B*)
   
6. \!\(\*OverscriptBox[\(Jx\), \(_\)]\)[p_, a_, b_] := (a \!\(\*OverscriptBox[\(b\), \(_\)]\) - \!\(\*OverscriptBox[\(a\), \(_\)]\) b + p (
   
7. \!\(\*OverscriptBox[\(a\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\)))/(a - b);
   
8. m = (b + c)/2; \!\(\*OverscriptBox[\(m\), \(_\)]\) = (\!\(\*OverscriptBox[\(b\), \(_\)]\) + \!\(\*OverscriptBox[\(c\), \(_\)]\))/2;(*M点是BC的中点*)
   
9. m1 = Simplify@Jx[m, a, j]; \!\(\*OverscriptBox[\(m1\), \(_\)]\) = Simplify@\!\(\*OverscriptBox[\(Jx\), \(_\)]\)[m, a, j];(*M1点是M点关于AJ的镜像点*)
   
10. Foot[p_, x_, y_] := ( \!\(\*OverscriptBox[\(x\), \(_\)]\) y - x \!\(\*OverscriptBox[\(y\), \(_\)]\) + (x - y) \!\(\*OverscriptBox[\(p\), \(_\)]\) + (\!\(\*OverscriptBox[\(x\), \(_\)]\) - \!\(\*OverscriptBox[\(y\), \(_\)]\)) p)/(2 (\!\(\*OverscriptBox[\(x\), \(_\)]\) -
    
11. \!\(\*OverscriptBox[\(y\), \(_\)]\)));  (* 从P点向XY直线引垂线，垂足的复坐标 *)
    
12. \!\(\*OverscriptBox[\(Foot\), \(_\)]\)[p_, x_, y_] := (x \!\(\*OverscriptBox[\(y\), \(_\)]\) - \!\(\*OverscriptBox[\(x\), \(_\)]\) y + (
    
13. \!\(\*OverscriptBox[\(x\), \(_\)]\) - \!\(\*OverscriptBox[\(y\), \(_\)]\)) p + (x - y) \!\(\*OverscriptBox[\(p\), \(_\)]\))/(2 (x - y));  
    
14. e = Simplify@Foot[b, a, c]; \!\(\*OverscriptBox[\(e\), \(_\)]\) = Simplify@\!\(\*OverscriptBox[\(Foot\), \(_\)]\)[b, a, c];
    
15. f = Simplify@Foot[c, b, a]; \!\(\*OverscriptBox[\(f\), \(_\)]\) = Simplify@\!\(\*OverscriptBox[\(Foot\), \(_\)]\)[c, b, a];
    
16. k[a_, b_] := (a - b)/(\!\(\*OverscriptBox[\(a\), \(_\)]\) - \!\(\*OverscriptBox[\(b\), \(_\)]\));(*定义复斜率*)
    
17. W1 = {p, \!\(\*OverscriptBox[\(p\), \(_\)]\)} /. Simplify@Solve[{(o - p) (\!\(\*OverscriptBox[\(o\), \(_\)]\) - \!\(\*OverscriptBox[\(p\), \(_\)]\)) == 1, k[a, p] == -1}, {p, \!\(\*OverscriptBox[\(p\), \(_\)]\)}] // Flatten;
    
18. p = Part[W1, 1]; \!\(\*OverscriptBox[\(p\), \(_\)]\) = Part[W1, 2];
    
19. W2 = {q, \!\(\*OverscriptBox[\(q\), \(_\)]\)} /. Simplify@Solve[{(o - q) (\!\(\*OverscriptBox[\(o\), \(_\)]\) - \!\(\*OverscriptBox[\(q\), \(_\)]\)) == 1, k[a, q] == k[a, m1]}, {q, \!\(\*OverscriptBox[\(q\), \(_\)]\)}] // Flatten;
    
20. q = Part[W2, 1]; \!\(\*OverscriptBox[\(q\), \(_\)]\) = Part[W2, 2];
    
21. Print["E = ", e, "，  F = ", f, "，  P = ", p, "，  Q = ", q];
    
22. Print["如果四边形EFPQ的两对边复斜率之积相等，则EFPQ四点共圆。"]
    
23. Print["测试EFPQ是否共圆："]
    
24. Simplify[k[e, f] k[p, q] == k[e, q] k[f, p]]

复制代码

天山草

对于 2# 楼 denglongshan 的程序解读如下：