|
|
概率导论P1.4
2.6 凯尔特人队和湖人队在季后赛中相遇, 双方要打 n 场比赛,其中 n 为奇数. 凯尔特人队赢一场球的概率为 p,而各次赢球是相互独立的.
(a) 求 p 的范围, 使得对于凯尔特人队来说, n=5 比 n=3 合算.
(b) 将(a)进行推广, 即对于任何 k 的值,找出 p 的范围使得 n=2k+1 比 n=2k-1 对
疑问:请看下方答案。这个P(A)的定义式应该如何理解?为什么是这三项相加?特别是加法第二项和第三项的含义是什么?
难道将P(A)定义为=\(\sum_{x=k+1}^{2k+1}C_{2k+1}^xp^x\left( 1-p\right)^{2k+1-x}\) 将P(B)定义为:\(\sum_{x=k}^{2k-1}C_{2k-1}^xp^x\left( 1-p\right)^{2k-1-x}\) 然后建立P(A)>P(B)的不等式来求P的范围不可以么?
答案:
We consider the general case of part (b), and we showthat p > 1/2 is a necessary and sufficient condition for n = 2k + 1 games to be betterthan n = 2k - 1 games. To prove this, let N be the number of Celtics’ wins in the first 2k-1 games. If A denotes the event that the Celtics win with n = 2k + 1, and B denotes the event that the Celtics win with n = 2k-1, then
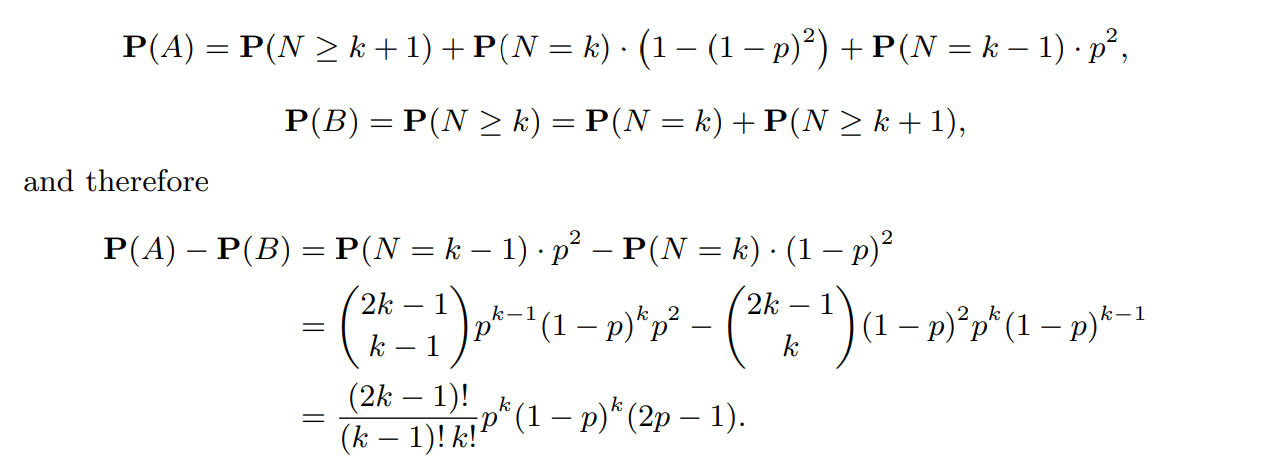
It follows that P(A) > P(B) if and only if p > 1/2. Thus, a longer series is better for the better team
|
|