丹尼尔·伯努利的共同生活的期望值与P无关？

wufaxian

《概率论导论》P147 31题

疑问：答案的公式推导没有任何疑问，疑问来自于答案最后一句话“does not depend on p”。p失去作用这件事情是否可以这样认为。当给定p和m以后，实际上获得了一个（2m，p）的二项分布。根据二项分布公式可以算出出“若干年”后或者的人数等于某个指定数值的概率。但是题目条件给出A=a 以后。二项分布公式的作用就消失了，此时P(A=a)=1  。此时p的作用就消失了。这道题此时真正跟“随机”有关的概率问题是剩下的a个人中1対夫妇健在的概率是多少。并据此算出1対夫妇健在的期望值，然后根据期望值的线性性质。算出m対 夫妇健在的期望值。

           如果以上理解正确。那么问题作一下延伸。在原题条件下是否可以认为“每一对夫妇健在”的概率是互相独立的？一对夫妇健在的概率是Q，Q= \(\frac{a\left( a-1\right)}{2m\left( 2m-1\right)}\)。那么幸存夫妇的概率分布是：\(C_m^x\ Q^x\left( 1-Q\right)^{m-x}\)   对么？


原题：
丹尼尔·伯努利的共同生活问题. 设有 m 对夫妻共同生活着.假定若干年以后每个人活着的概率为 p, 并且彼此相互独立.记 A 为若干年后活着的人数, S 为若干年后夫妻都活着的对数.对任何 a, 求 E[S|A=a]


答案：
Let Xi be the random variable taking the value 1 or 0 depending on whether the first partner of the ith couple has survived or not. Let Yi be the corresponding random variable for the second partner of the ith couple. Then,we have S =\(\sum_{i=1}^mE\left[ X_iY_i|A=a\right]\) , and by using the total expectation theorem,

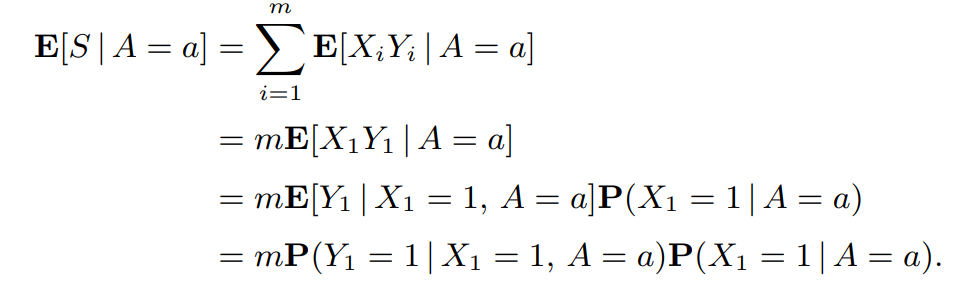
justinyang948

A=a的条件下，您说的没错。